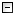## Dynamic Factor Model
## Simulated 6v2f data with ar(1) factors
# DAFS model with AR(1)
model{
# Model-relationship between observed variables and factors
for (t in 1:T){
for (p in 1:P){
y[t,p]~dnorm(mu[t,p],pre_e[p])
}
for (p in 1:3){
mu[t,p]<-lam[p]*f[t,1]
}
for (p in 4:6){
mu[t,p]<-lam[p]*f[t,2]
}
}
## Autoregression of factors
for (t in 2:T){
f[t,1:2]~dmnorm(muf[t,1:2],pre_v[1:2,1:2])
muf[t,1]<-b[1]*f[t-1,1]+b[2]*f[t-1,2]
muf[t,2]<-b[3]*f[t-1,1]+b[4]*f[t-1,2]
}
f[1,1:2]~dmnorm(muf[1,1:2], pre_v[1:2,1:2])
muf[1,1]<-b[1]*f0[1]+b[2]*f0[2]
muf[1,2]<-b[3]*f0[1]+b[4]*f0[2]
f0[1]~dnorm(0,.0001)
f0[2]~dnorm(0,.0001)
pre_v[1:2,1:2]<-inverse(cov_v[1:2,1:2])
cov_v[1,1]<-.36
cov_v[2,2]<-.36
cov_v[1,2]<-cov_v[2,1]
cov_v[2,1]~dunif(0,1)
##Prior distribution
for (p in 1:P){
pre_e[p]~dgamma(.001,.001)
}
for (p in 1:6){
lam[p]~dnorm(0,.001)}
for (i in 1:4){
b[i]~dnorm(0,.001)
}
for (p in 1:6){
Par[p]<-lam[p]
Par[6+p]<-1/pre_e[p]
}
for (i in 1:4){
Par[12+i]<-b[i]
}
Par[17]<-cov_v[2,1]
}
starting values
list(b=c(.8,0,0,.8), pre_e=c(10,10,10,10,10,10), lam=c(1,1,1,1,1,1))
list( T=150, P=6, list(y = structure(.Data = c(
0.1748170693,0.6367873144,0.0248632848,-..., -1.867119034,-1.206459092,-0.615199296),
.Dim = c(150, 6)))